

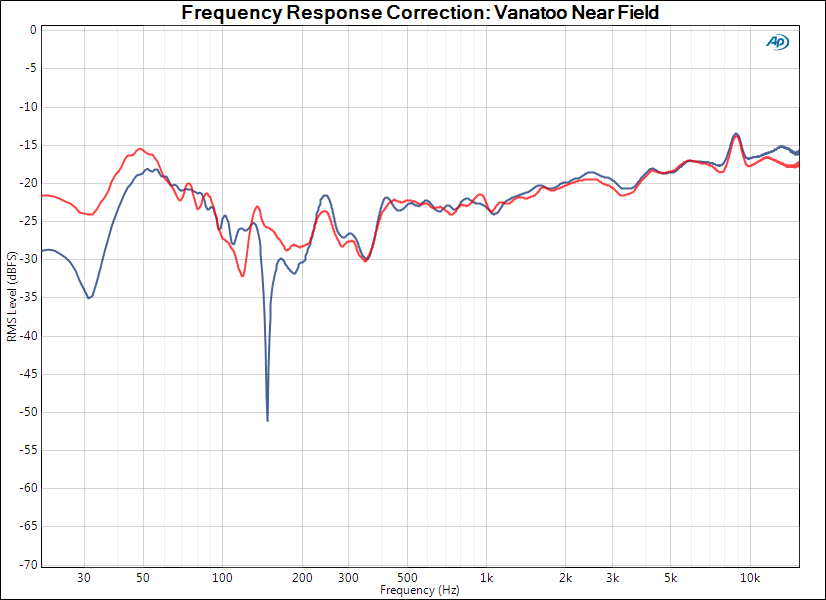
So if you need to implement a high-pass filter or derivative-like filter (or even band-pass), then you must go for types 3 and 4. The filters with anti-symmetrical impulse response all have a zero at $z=1$ (i.e. In these cases type I or type III filters are preferred.
In some applications an integer group delay is desirable. They are well suited for differentiators and Hilbert transformers, and their magnitude approximation is usually better because, unlike type III filters, they have no zero at $z=-1$. Type IV filters cannot be used for standard frequency selective filters, for the same reasons as type III filters. On the other hand, a type III Hilbert transformer can be implemented more efficiently than a type IV Hilbert transformer because in this case every other tap is zero. For Hilbert transformers, type III filters have a relatively bad magnitude approximation at very low and very high frequencies due to the zeros at $z=1$ and $z=-1$. Type III filters cannot be used for standard frequency selective filters because in these cases the 90 degrees phase shift is usually undesirable. Neither can they be used for applications where a 90 degrees phase shift is necessary. Type II filters would normally not be used for high pass or band stop filters, due to the zero at $z=-1$, i.e. for differentiators or Hilbert transformers. Type I filters are pretty universal, but they cannot be used whenever a 90 degrees phase shift is necessary, e.g. This implies (among other things) the following: Type IV filters (even number of taps, odd symmetry) always have a zero at $z=1$, a phase shift of 90 degrees, and a non-integer group delay. at $f=0$ and $f=f_s/2$), they have a 90 degrees phase shift, and an integer group delay.

Type III filters (odd number of taps, odd symmetry) always have zeros at $z=1$ and $z=-1$ (i.e. Type II filters (even number of taps, even symmetry) always have a zero at $z=-1$ (i.e., half the sampling frequency), they have a zero phase shift, and they have a non-integer group delay. Phase shift (apart from the linear phase)įor type I filters (odd number of taps, even symmetry) there are no constraints on the zeros at $z=1$ and $z=-1$, the phase shift is zero (apart from the linear phase), and the group delay is an integer value. When choosing one of these 4 types of linear phase filters there are mainly 3 things to consider:Ĭonstraints on the zeros of $H(z)$ at $z=1$ and $z=-1$


 0 kommentar(er)
0 kommentar(er)
